Leetcode 33: Search in Rotated Sorted Array

The original question can be found here.

The question is asking us to find a target element in rotated sorted array. Since the question is explictly asking for a O(logn) solution, so let’s jump to the binary search solution.

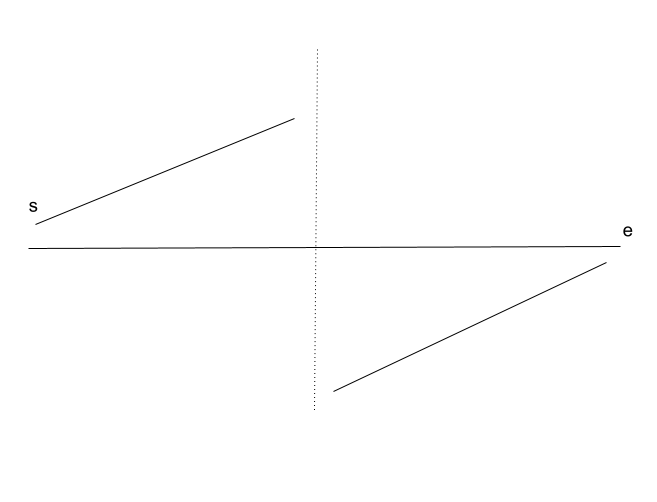
After rotation, the array is in 2 parts: Both left and right parts are in ascending order. However, elements in left part are larger than in right part.

Binary Search for 2 Times

Since the question is explictly asking us for a O(logn) solution, we need to use binary search. First we can figure out which part of array that element might be in, and then we do regular binary search on that part. We’re doing this by first finding the index of smallest element’s index, and then compare the target with last element. If target is no larger than last element, we go to right part. Otherwise, we go to left part:

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        smallest_element_index = self.find_min(nums)
        if target <= nums[len(nums) - 1]:
            return self.binary_search(nums, smallest_element_index, len(nums) - 1, target)
        else:
            return self.binary_search(nums, 0, smallest_element_index - 1, target)

    def binary_search(self, nums: List[int], start: int, end: int, target: int) -> int:
        while start + 1 < end:
            mid = (start + end) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                start = mid
            else:
                end = mid
        
        if nums[start] == target:
            return start
        
        if nums[end] == target:
            return end

        return -1
    
    def find_min(self, nums: List[int]) -> int:
        left, right = 0, len(nums) - 1
        end = right
        while left + 1 < right:
            mid = (left + right) // 2
            if nums[mid] < nums[end]:
                right = mid
            else:
                left = mid
        return left if nums[left] < nums[right] else right

Time Complexity: O(logn). Space Complexity: O(1).

Binary Search for 1 Time

The interviewer might be asking: Can you do it with just 1 binary search? Sure we can. Once we get middle element and compare it with target, we get following cases:

When nums[mid]is at left part:

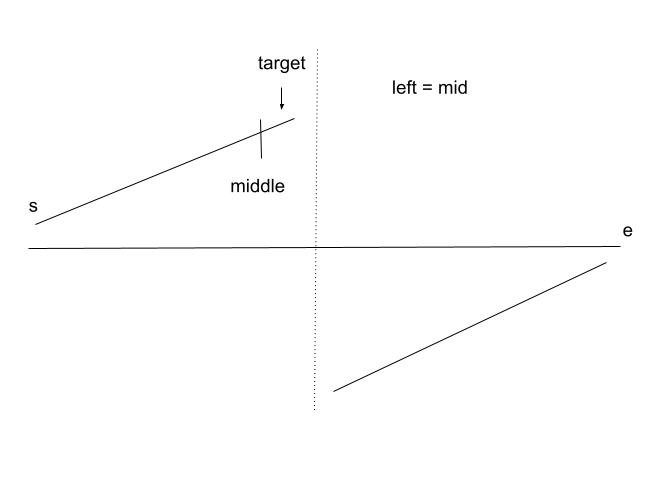
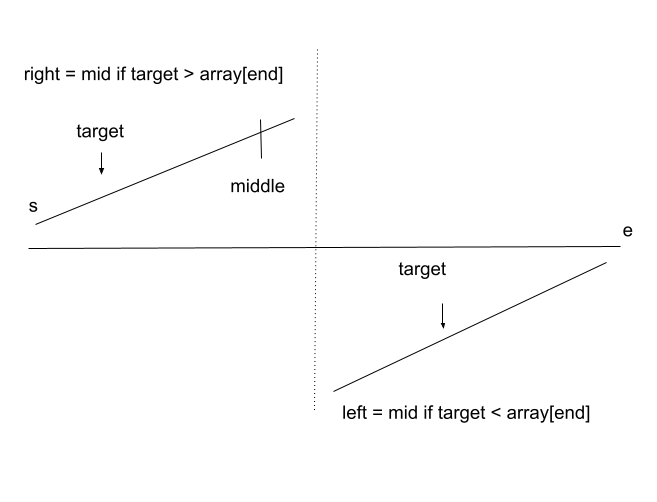
When nums[mid] > target:

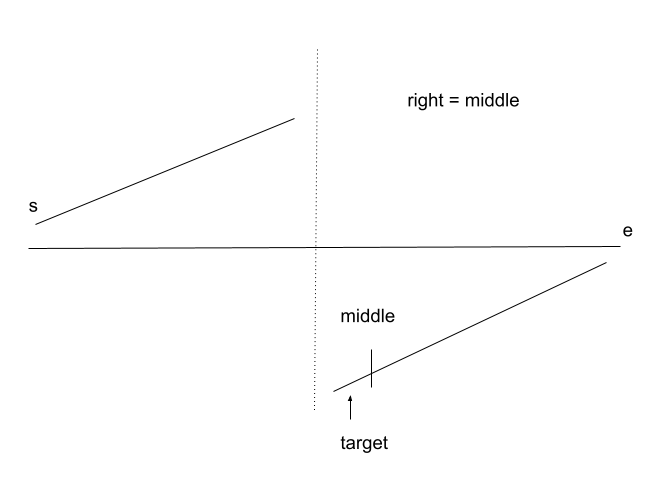
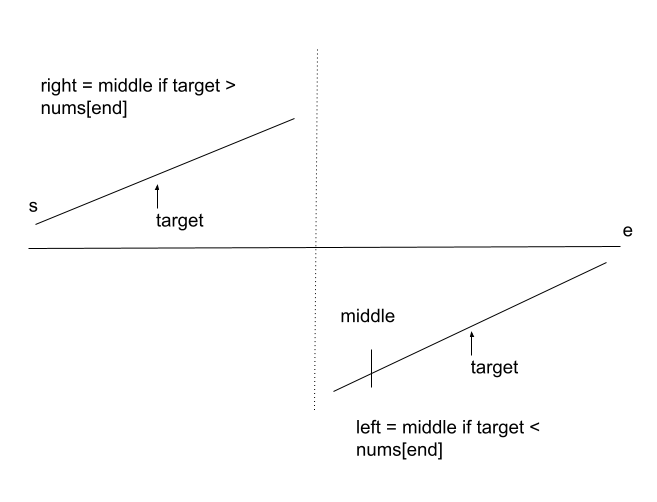
Put together:

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        start, end = 0, len(nums) - 1
        while left + 1 < right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            if nums[mid] < target:
                if nums[mid] > nums[end]:
                    left = mid
                else:
                    if target <= nums[end]:
                        left = mid
                    else:
                        right = mid
            else:                               
                if nums[mid] < nums[end]:
                    right = mid
                else:
                    if target <= nums[end]:
                        left = mid
                    else:
                        right = mid
        
        if nums[left] == target:
            return left

        if nums[right] == target:
            return right

        return -1

Time complexity: O(logn). Space complexity: O(1).