Leetcode 81: Search in Rotated Sorted Array II

The original question can be found here.

The question is asking us to check if target is in a rotated sorted array. Here the array can have duplicate numbers.

Brute Force

The brute force solution is scanning the whole array to find the target element:

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        for num in nums:
            if num == target:
                return True

        return False

Time Complexity: O(n). Space Complexity: O(1).

Binary Search

This question is very tricky because there’re some situations we cannot apply binary search directly. Recall from Search in Rotated Sorted Array I, we compare the middle element with target and end element to determine which part of array we’ll explore next. However, in this question, since the element can be duplicated, let’s say when we meet this case:

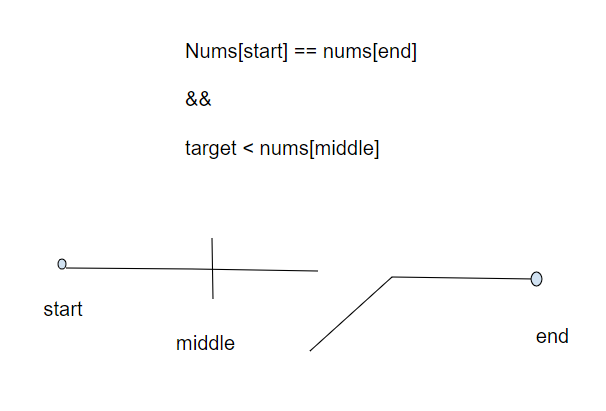
Let’s say target < nums[middle], we have to know which part that the middle element is in, since if target < nums[middle], it could be either [start, middle], or [middle, end]. Then we need to compare middle element with end element, if nums[middle] > nums[end], we know it’s on left part, thus if nums[start] <= target < nums[middle], we go [start, middle], otherwise [middle, end], etc..

However, in the case above, we cannot tell which part middle element is at since nums[start] == nums[end], thus we cannot apply binary search. Instead, we can shrink the start or end boundary until they’re different, then we can apply binary search again.

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        start, end = 0, len(nums) - 1
        while start + 1 < end:
            while nums[start] == nums[end] and start + 1 < end:
                start += 1
            if start + 1 >= end:
                break
            mid = (start + end) // 2
            if nums[mid] == target:
                return True
            if nums[mid] > nums[end]:
                if nums[start] <= target < nums[mid]:
                    end = mid
                else:
                    start = mid
            else:
                if nums[mid] < target <= nums[end]:
                    start = mid
                else:
                    end = mid

        return True if nums[start] == target or nums[end] == target else False

Time Complexity: best case O(logn), worst case O(n) if all elements are same. Space Complexity: O(1).